The “golden moment”

We’re in final exams week right now, and last night students in the MATLAB course took their exam. It included some essay questions asking for their favorite elements of the course and things that might be improved in the course. I loved what one of my students had to say about the assignment in the course he found to be the most interesting, so I’ve gotten permission from him to share it. The lab problem he’s referring to was to write a MATLAB program to implement the bisection method for polynomials.

It is really hard to decide which project I found most interesting; there are quite a few of them. If I had to choose just one though, I would probably have to say the lab set for April 6. I was having a really hard time getting the program to work, I spent a while tweaking it this way and that way. But when you’re making a program that does not work yet, there is this sort of golden moment, a moment when you realize what the missing piece is. I remember that moment on my April 6 lab set. After I realized what it was, I could not type it in fast enough I was so excited just to watch the program work. After hitting the play button, that .3 seconds it takes for MATLAB to process the program felt like forever. I actually was devastated that I got an error, and thought I had done it all wrong once again, but then I remembered I had entered the error command so it would display an error. I actually started laughing out loud in the lab, quite obnoxiously actually.

Yes!  As somebody once said, true learning consists in the debugging process. And that’s where the fun in learning happens to lie, too. Let’s give students as many shots as possible to experience this process themselves.

The inverted classroom and student self-image

Image via Wikipedia

This week I’ve been immersed in the inverted classroom idea. First, I gave this talk about an inverted linear algebra classroom at the Joint Meetings in New Orleans and had a number of really good conversations afterwards about it. Then, this really nice writeup of an interview I gave for MIT News came out, highlighting the relationship between my MATLAB course and the MIT OpenCourseware Project. And this week, I’ve been planning out the second iteration of that MATLAB course that’s starting in a few weeks, hopefully with the benefit of a year’s worth of experience and reflection on using the inverted classroom to teach technical computing to novices.

One thing that I didn’t talk much about at the Joint Meetings or in the MIT interview was perhaps the most prominent thing about using the inverted classroom model on a day-to-day basis: how students react to it and change as a result of it. I was actually quite surprised that nobody at my Joint Meetings talk asked me a question about this, because honestly, the inverted classroom sounds great on paper, but when you start to imagine the average college student walking in on the first day of class and having this method of instruction described to him, it becomes clear that a significant amount of work is going to have to be done in order to get students — who are already resistant to any change from their accustomed modes of instruction — on board with the plan.

Students do tend to resist the inverted classroom at first. Some forms of resistance are more benign than others. On the benign end of the spectrum there are students with little experience with the course material or its prerequisites who get bogged down on the basic podcast viewing (which takes the place of in-class lectures in this model) or the accompanying guided practice, and instead of actively seeking a resolution to their question will wait for the instructor to clear it up — in class. On the other end is the student who simply doesn’t believe I’m serious when I say there won’t be any lecturing, who then doesn’t do the work, assuming I’ll bail him out somehow — in class. But in the inverted model, students are held responsible for acquiring basic competencies before class so that the hard stuff — what we refer to as assimilation — is the primary focus of the class time.

I break this distinction down for students, but not everybody buys into it. Those who don’t will have to undergo a learning process that usually looks like shock — shock that I won’t reteach them the material they were supposed to have viewed and worked on, while the lab assignment based on that material is going on. This can get very ugly in ways I probably don’t need to describe. Let’s just say that you had better not use the inverted classroom model if you aren’t prepared to put out a constant P.R. effort to convince students of the positive benefits of the model and constantly to assuage student concerns.

I’ve often wondered why students sometimes react so negatively to the inverted classroom model. I’ve come to believe it’s the result of a invasive, false belief that can arise in students about their ability to learn things independently of others — namely, that they simply cannot do so. I have had students tell me this to my face — “I can’t learn [insert topic] unless you lecture to me about it in class first.” Clearly this is not true. Toddlers learn their native language without formal instruction, just by assimilating (there’s that word again) the language going on naturally in their background. We all learn things every day without sitting in a classroom; we may seek out training data first through printed instructions, worked-out examples, YouTube videos, etc., but it’s almost never in a classroom setting. Learning new things on our own initiative and without formal instruction in a classroom setting is as natural to humans as breathing. Indeed you could say that it’s the capacity to learn in this way that makes us human. But somehow many students think otherwise.

Where does this belief come from? I think that it comes from its own instance of assimilation, namely the assimilation of a culture of programmed classroom instruction that takes place from roughly the first grade through the twelfth grade in this country. Students have so few experiences where they pursue and construct their own knowledge that they simply come to believe that they are incapable of doing so. And this belief is propagated most rapidly in mathematics. I’ve been reading in Seymour Papert‘s book Mindstorms: Children, Computers, and Powerful Ideas, and this quote hits this issue right on the head:

Difficulty with school math is often the first step of an invasive intellectual process that leads us all to define ourselves as bundles of aptitudes and ineptitudes, as being “mathematical” or “not mathematical”, “artistic” or “not artistic”, “musical” or “not musical”, “profound” or “superficial”, “intelligent” or “dumb”. Thus deficiency becomes identity and learning is transformed from the early child’s free exploration of the world to a chore beset by insecurities and self-imposed restrictions.

That last sentence (emphasis added) sums it up, doesn’t it? Deficiency becomes identity. Eventually, if a student is robbed of experiences of self-motivated learning, the student eventually adopts a self-image in which she is incapable of self-motivated learning. It is a false self-image that is ultimately dehumanizing.

Which is why I put such stock in the inverted classroom model. I think this method of teaching, along with other learner-centered modes of instruction like problem-based learning, is on the front lines in reversing students’ negative ways of thinking about how they learn. Students may (will?) chafe at the inversion at first. But in the MATLAB course at least, something really cool happened at the end of the semester. I made up a slideshow for students called “Five myths about how you think you learn that CMP 150 has busted”. Among the myths were “I can’t learn unless a professor lectures to me” and “I can’t learn on my own initiative”, and I gave concrete examples of work that the students had done in the class that contradicted these messages. In the end I showed them that through this inverted classroom process they had taken majors strides toward being confident, independent, skill learners and problem-solvers rather than just people who can play the classroom game well. And even the most skeptical students were nodding in agreement. And I think that makes it all worthwhile for everyone.

A problem with “problems”

I have a bone to pick with problems like the following, which is taken from a major university-level calculus textbook. Read it, and see if you can figure out what I mean.

This is located in the latter one-fourth of a review set for the chapter on integration. Its position in the set suggests it is less routine, less rote than one of the early problems. But what’s wrong with this problem is that it’s not a problem at all. It’s an exercise. The difference between the two is enormous. To risk oversimplifying, in an exercise, the person doing the exercise knows exactly what to do at the very beginning to obtain the information being requested. In a problem, the person doesn’t. What makes an exercise an exercise is its familiarity and congruity with prior exercises. What makes a problem a problem is the lack of these things.

The above is not a problem, it is an exercise. Use the Midpoint Rule with six subintervals from 0 to 24. That’s the only part of the statement that you even have to read! The rest of it has absolutely nothing with bees, the rate of their population growth, or the net amount of population growth. A student might be turning this in to an instructor who takes off points for incorrect or missing units, and then you have to think about bees and time. Otherwise, this exercise is pure pseudocontext.

Worst of all, this exercise might correctly assess students’ abilities to execute a numerical integration algorithm, but it doesn’t come close to measuring whether a student understands what an integral is in the first place and why we are even bringing them up. Even if the student realizes an integral should be used, there’s no discussion of how to choose which method and which parameters within the method, or why. Instead, the exercise flatly tells students not only to use an integral, but what method to use and even how many subdivisions. A student can get a 100% correct answer and have no earthly idea what integration has to do with the question.

A simple fix to the problem statement will change this into a problem. Keep the graph the same and change the text to:

The graph below shows the rate at which a population of honeybees was growing, in bees per week. By about how many bees did the population grow after 24 weeks?

This still may not be a full-blown problem yet — and it’s still pretty pseudocontextual, and the student can guess there should be an integral happening because it’s in the review section for the chapter on integration —  but at least now we have to think a lot harder about what to do, and the questions we have to answer are better. How do I get a total change when I’m given a rate? Why can’t I just find the height of the graph at 24? And once we realize that we have to use an integral — and being able to make that realization is one of the main learning objectives of this chapter, or at least it should be — there are more questions. Can I do this with an antiderivative? Can I use geometry in some way? Should I use the Midpoint Rule or some other method? Can I get by with, say, six rectangles? or four? or even two? Why not use 24, or 2400? Is it OK just the guesstimate the area by counting boxes?

I think we who teach calculus and those who write calculus books must do a better job of giving problems to students and not just increasingly complicated exercises. It’s very easy to do so; we just have to give less information and fewer artificial cues to students, and force students to think hard and critically about their tools and how to select the right combination of tools for the job. No doubt, this makes grading harder, but students aren’t going to learn calculus in any real or lasting sense if they don’t grapple with these kinds of problems.

What correlates with problem solving skill?

About a year ago, I started partitioning up my Calculus tests into three sections: Concepts, Mechanics, and Problem Solving. The point values for each are 25, 25, and 50 respectively. The Concepts items are intended to be ones where no calculations are to be performed; instead students answer questions, interpret meanings of results, and draw conclusions based only on graphs, tables, or verbal descriptions. The Mechanics items are just straight-up calculations with no context, like “take the derivative of “. The Problem-Solving items are a mix of conceptual and mechanical tasks and can be either instances of things the students have seen before (e.g. optimzation or related rates problems) or some novel situation that is related to, but not identical to, the things they’ve done on homework and so on.

I did this to stress to students that the main goal of taking a calculus class is to learn how to solve problems effectively, and that conceptual mastery and mechanical mastery, while different from and to some extent independent of each other, both flow into mastery of problem-solving like tributaries to a river. It also helps me identify specific areas of improvement; if the class’ Mechanics average is high but the Concepts average is low, it tells me we need to work more on Concepts.

I just gave my third (of four) tests to my two sections of Calculus, and for the first time I started paying attention to the relationships between the scores on each section, and it felt like there were some interesting relationships happening between the sections of the test. So I decided to do not only my usual boxplot analysis of the individual parts but to make three scatter plots, pairing off Mechanics vs. Concepts, Problem Solving vs. Concepts, and Mechanics vs. Problem Solving, and look for trends.

Here’s the plot for Mechanics vs. Concepts:

That r-value of 0.6155 is statistically significant at the 0.01 level. Likewise, here’s Problem Solving vs. Concepts:

The r-value here of 0.5570 is obviously less than the first one, but it’s still statistically significant at the 0.01 level.

But check out the Problem Solving vs. Mechanics plot:

There’s a slight upward trend, but it looks disarrayed; and in fact the r = 0.3911 is significant only at the 0.05 level.

What all this suggests is that there is a stronger relationship between conceptual knowledge and mechanics, and between conceptual knowledge and problem solving skill, than there is between mechanical mastery and problem solving skill. In other words, while there appears to be some positive relationship between the ability simply to calculate and the ability to solve problems that involve calculation (are we clear on the difference between those two things?), the relationship between the ability to answer calculus questions involving no calculation and the ability to solve problems that do involve calculation is stronger — and so is the relationship between no-calculation problems and the ability to calculate, which seems really counterintuitive.

If this relationship holds in general — and I think that it does, and I’m not the only one — then clearly the environment most likely to teach calculus students how to be effective problem solvers is not the classroom primarily focused on computation. A healthy, interacting mixture of conceptual and mechanical work — with a primary emphasis on conceptual understanding — would seem to be what we need instead. The fact that this kind of environment stands in stark contrast to the typical calculus experience (both in the way we run our classes and the pedagogy implied in the books we choose) is something well worth considering.

Calculus and conceptual frameworks

Image via http://www.flickr.com/photos/loopzilla/

I was having a conversation recently with a colleague who might be teaching a section of our intro programming course this fall. In sharing my experiences about teaching programming from the MATLAB course, I mentioned that the thing that is really hard about teaching programming is that students often lack a conceptual framework for what they’re learning. That is, they lack a mental structure into which they can place the topics and concepts they’re learning and then see those ideas in their proper place and relationship to each other. Expert learners — like some students who are taking an intro programming course but have been coding since they were 6 years old — have this framework, and the course is a breeze. Others, possibly a large majority of students in a class, have never done any kind of programming, and they will be incapable of really learning programming until they build a conceptual framework to  handle it. And it’s the prof’s job to help them build it.

Afterwards, I thought, this is why teaching intro programming is harder than teaching calculus. Because students who make it all the way into a college calculus surely have a well-developed conceptual framework for mathematics and can understand where the topics and methods in calculus should fit. Right? Hello?

It then hit me just how wrong I was. Students coming into calculus, even if they’ve had the course before in high school, are not guaranteed to have anything like an appropriate conceptual framework for calculus. Some students may have no conceptual framework at all for calculus — they’ll be like intro programming students who have never coded — and so when they see calculus concepts, they’ll revert back to their conceptual frameworks built in prior math courses, which might be robust and might not be. But even then, students may have multiple, mutually contradictory frameworks for mathematics generally owing to different pedagogies, curricula, or experiences with math in the past.

Take, for example, the typical first contact that calculus students get with actual calculus in the Stewart textbook: The tangent problem. The very first example of section 2.1 is a prototype of this problem, and it reads: Find an equation of the tangent line to the parabola at the point . What follows is the usual initial solution: (1) pick a point near , (2) calculate the slope of the secant line, (3) move closer to and recalculate, and then (4) repeat until the differences between successive approximations dips below some tolerance level.

What is a student going to do with this example? The ideal case — what we think of as a proper conceptual handling of the ideas in the example — would be that the student focuses on the nature of the problem (I am trying to find the slope of a tangent line to a graph at a point), the data involved in the problem (I am given the formula for the function and the point where the tangent line goes), and most importantly the motivation for the problem and why we need something new (I’ve never had to calculate the slope of a line given only one point on it). As the student reads the problem, framed properly in this way, s/he learns: I can find the slope of a tangent line using successive approximations of secant lines, if the difference in approximations dips below a certain tolerance level. The student is then ready for example 2 of this section, which is an application to finding the rate at which a charge on a capacitor is discharged. Importantly, there is no formula for the function in example 2, just a graph.

But the problem is that most students adopt a conceptual framework that worked for them in their earlier courses, which can be summarized as: Math is about getting right answers to the odd-numbered exercises in the book. Students using this framework will approach the tangent problem by first homing in on the first available mathematical notation in the example to get cues for what equation to set up. That notation in this case is:

Then, in the line below, a specific value of x (1.5) is plugged in. Great! they might think, I’ve got a formula and I just plug a number into it, and I get the right answer: 2.5. But then, reading down a bit further, there are insinuations that the right answer is not 2.5. Stewart says, “…the closer is to 1…it appears from the tables, the closer is to 2. This suggests that the slope of the tangent line should be .” The student with this framework must then be pretty dismayed. What’s this about “it appears” the answer is 2? Is it 2, or isn’t it? What happened to my 2.5? What’s going on? And then they get to example 2, which has no formula in it at all, and at that point any sane person with this framework would give up.

It’s also worth noting that the Stewart book — and many other standard calculus books — do not introduce this tangent line idea until after a lengthy precalculus review chapter, and that chapter typically looks just like what students saw in their Precalculus courses. These treatments do not attempt to be a ramp-up into calculus, and presages of the concepts of calculus are not present. If prior courses didn’t train students on good conceptual frameworks, then this review material actually makes matters worse when it comes time to really learn calculus. They will know how to plug numbers and expressions into a function, but when the disruptively different math of calculus appears, there’s nowhere to put it, except in the plug-and-chug bin that all prior math has gone into.

So it’s extremely important that students going into calculus get a proper conceptual framework for what to do with the material once they see it. Whose responsibility is that? Everybody’s, starting with…

• the instructor. The instructor of a calculus class has to be very deliberate and forthright in bending all elements of the course towards the construction of a framework that will support the massive amount of material that will come in a calculus class. This includes telling students that they need a conceptual framework that works, and informing them that perhaps their previous frameworks were not designed to manage the load that’s coming. The instructor also must be relentless in helping students put new material in its proper place and relationship to prior material.
• But here the textbooks can help, too, by suggesting the framework to be used; it’s certainly better than not specifying the framework at all but just serving up topic after topic as non sequiturs.
• Finally, students have to work at constructing a framework as well; and they should be held accountable not only for their mastery of micro-level calculus topics like the Chain Rule but also their ability to put two or more concepts in relation to each other and to use prior knowledge on novel tasks.

What are your experiences with helping students (in calculus or otherwise) build useable conceptual frameworks for what they are learning? Any tools (like mindmapping software), assessment methods, or other teaching techniques you’d care to share?

Boxplots: Curiouser and curiouser

The calculus class took their third (and last) hour-long assessment yesterday. In the spirit of data analytics ala the previous post here, I made boxplots for the different sections of the test (Conceptual Knowledge (CK), Computation (C), and Problem Solving (PS)) as well as the overall scores. Here are the boxplots for this assessment — put side-by-side with the boxplots for the same sections on the previous assessments. “A2” and “A3” mean Assessments 2 and 3.

Obviously there is still a great deal of improvement to be had here — the fact that the class average is still below passing remains unacceptable to me — but there have been some definite gains, particularly in the conceptual knowledge department.

What changed between Assessment 2 and Assessment 3? At least three things:

• The content changed. Assessment 2 was over derivative rules and applications; Assessment 3 covered integration.
• The way I treated the content in class changed. Based on the results of Assessment 2, I realized I needed to make conceptual work a much greater part of the class meetings. Previously the class meetings had been about half lecture, with time set aside to work “problems” — meaning, exercises, such as “find the critical numbers of . Those are not really problems that assess conceptual knowledge. So I began to fold in more group work problems that ask students to reason from something other than a calculation. I stressed these problems from the textbook more in class. I tried to include more such problems in WeBWorK assignments — though there are precious few of them to be had.
• The level of lip service I gave to conceptual problems went up hugely. Every day I was reminding the students of the low scores on Conceptual Knowledge on the test and that the simplest way to boost their grades in the class would be to improve their conceptual knowledge. I did not let their attention leave this issue.

Somewhere in a combination of these three things we have the real reason those scores went up. I tend to think the first point had little to do with it. Integration doesn’t seem inherently any easier to understand conceptually than differentiation, particularly at this stage in the course when differentiation is relatively familiar and integration is brand new. So I think that simply doing more conceptual problems in class and stressing the importance of conceptual knowledge in class were the main cause of the improvements.

Quite interestingly, the students’ scores on computation also improved — despite the reduced presence of computation in class because of the ramped-up levels of conceptual problems. We did fewer computational problems on the board and in group work, and yet their performance on raw computation improved! Again, I don’t think integration is easier than differentiation at this stage in the course, so I don’t think this improvement was because the material got easier. Maybe the last test put the fear of God into them and they started working outside of class more. I don’t know. But this does indicate to me that skill in computation is not strictly proportional to the amount of computation I do, or anybody else does, in class.

To overgeneralize for a second: Increased repetition on conceptual problems improves performance on those problems dramatically, while the corresponding reduction in time spent on computational exercises not only does not harm students’ performance on computation but might actually have something to do with improving it. If we math teachers can understand the implications of this possibility (or at least understand the extent to which this statement is true) we might be on to something big.

The scores on problem solving went two different directions. On the one hand, the median went up; but on the other hand the mean went down. And the middle 50% didn’t get any better on the top end and got worse on the bottom end. I’m still parsing that out. It could be the content itself this time; most of the actual problems in integration tend to take place near the end of the chapter, after the Fundamental Theorem and u-substitution, so the kinds of problems in this section were less than a week old for these students. But quite possibly the improvement in conceptual knowledge brought the median up on problem solving, despite the newness of the problems. Or maybe the differences aren’t even statistically significant.

What I take away from this is that if you want students to do well on non-routine problems, those problems have to occupy a central place in the class, and they have to be done not outside of class where there’s no domain expert to guide the students through them but in class. And likewise, we need not worry so much that we are “wasting precious class time” on group work on conceptual problems at the expense of individual computation skill. Students might do just fine on that stuff regardless, perhaps even better if they have enhanced conceptual understanding to support their computational skills.

It all goes back to support the inverted classroom model which I’ve been using in the MATLAB course, and now I’m wondering about its potential in calculus as well.

The case of the curious boxplots

I just graded my second hour-long assessment for the Calculus class (yes, I do teach other courses besides MATLAB). I break these assessments up into three sections: Concept Knowledge, where students have to reason from verbal, graphical, or numerical information (24/100 points); Computations, where students do basic context-free symbol-crunching (26/100 points); and Problem Solving, consisting of problems that combine conceptual knowledge and computation (50/100 points). Here’s the Assessment itself. (There was a problem with the very last item — the function doesn’t have an inflection point — but we fixed it and students got extra time because of it.)

Unfortunately the students as a whole did quite poorly. The class average was around a 51%. As has been my practice this semester, I turn to data analysis whenever things go really badly to try and find out what might have happened. I made boxplots for each of the three sections and for the overall scores. The red bars inside the boxplots are the averages for each.

I think there’s some very interesting information in here.

The first thing I noticed was how similar the Calculations and Problem Solving distributions were. Typically students will do significantly better on Calculations than anything else, and the Problem Solving and Concept Knowledge distributions will mirror each other. But this time Calculations and Problem Solving appear to be the same.

But then you ask: Where’s the median in boxplots for these two distributions? The median shows up nicely in the first and fourth plot, but doesn’t appear in the middle two. Well, it turns out that for Calculations, the median and the 75th percentile are equal; while for Problem Solving, the median and the 25th percentile are equal! The middle half of each distribution is between 40 and 65% on each section, but the Calculation middle half is totally top-heavy while the Problem Solving middle half is totally bottom-heavy. Shocking — I guess.

So, clearly conceptual knowledge in general — the ability to reason and draw conclusions from non-computational methods — is a huge concern. That over 75% of the class is scoring less than 60% on a fairly routine conceptual problem is unacceptable. Issues with conceptual knowledge carry over to problem solving. Notice that the average on Conceptual Knowledge is roughly equal to the median on Problem Solving. And problem solving is the main purpose of having students take the course in the first place.

Computation was not as much of an issue for these students because they get tons of repetition with it (although it looks like they could use some more) via WeBWorK problems, which are overwhelmingly oriented towards context-free algebraic calculations. But what kind of repetition and supervised practice do they get with conceptual problems? We do a lot of group work, but it’s not graded. There is still a considerable amount of lecturing going on during the class period as well, and there is not an expectation that when I throw out a conceptual question to the class that it is supposed to be answered by everybody. Students do not spend nearly as much time working on conceptual problems and longer-form contextual problems as they do basic, context-free computation problems.

This has got to change in the class, both for right now — so I don’t end up failing 2/3 of my class — and for the future, so the next class will be better equipped to do calculus taught at a college level. I’m talking with the students tomorrow about the short term. As for the long term, two things come to mind that can help.

• Clickers. Derek Bruff mentioned this in a Twitter conversation, and I think he’s right — clickers can elicit serious work on conceptual questions and alert me to how students are doing with these kinds of questions before the assessment hits and it’s too late to do anything proactive about it. I’ve been meaning to take the plunge and start using clickers and this might be the right, um, stimulus for it.
• Inverted classroom. I’m so enthusiastic about how well the inverted classroom model has worked in the MATLAB course that I find myself projecting that model onto everything. But I do think that this model would provide students with the repetition and accountability they need on conceptual work, as well as give me the information about how they’re doing that I need. Set up some podcasts for course lectures for students to listen/watch outside of class; assign WeBWorK to assess the routine computational problems (which would be no change from what we’re doing now); and spend every class doing a graded in-class activity on a conceptual or problem-solving activity. That would take some work and a considerable amount of sales pitching to get students to buy into it, but I think I like what it might become.

Active learning is essential, not optional, for STEM students

This article (1.2 MB, PDF)  by three computer science professors at Miami University (Ohio) is an excellent overview of the concept of the inverted classroom and why it could be the future of all classrooms given the techno-centric nature of Millenials. (I will not say “digital natives”.) The article focuses on using inverted classroom models in software engineering courses. This quote seemed particularly important:

Software engineering is, at its essence, an applied discipline that involves interaction with customers, collaboration with globally distributed developers, and hands-on production of software artifacts. The education of future software engineers is, by necessity, an endeavor that requires students to be active learners. That is, students must gain experience, not in isolation, but in the presence of other learners and under the mentorship of instructors and practitioners.  [my emphasis]

That is, in the case of training future software engineers, active learning is not an option or a fad; it is essential, and failure to train software engineers in an active learning setting is withholding from them the essential mindset they will need for survival in their careers. If a software engineer isn’t an active learner, they won’t make it — the field is too fast-moving, too global, too collaborative in its nature to support those who can only learn passively. Lectures and other passive teaching techniques may not be obsolete, but to center students’ education around this kind of teaching sets the students up for failure later on.

One could argue the same thing for any kind of engineer, or any of the STEM disciplines in general, since careers in those disciplines tend to adhere to the same description as software engineering — a tendency toward applications (many of which don’t even exist yet), centered on interaction and collaboration with people, and focused on the production of usable products.

Turning questions into learning

Image by CarbonNYC via Flickr

The hardest thing about teaching the MATLAB course — or any course — is responding to student questions. Notice I do not say “answering” student questions. Answers are not the issue; I’m no MATLAB genius, but I can answer 95% of student questions on the spot. The real issue is whether I should. If my primary task is to teach students habits of mind that translate into lifelong learning — and I earnestly believe that it is — then answers are not always the best thing for students.

I’ve noticed four types of questions that students tend to ask in the MATLAB course, and these carry over pretty seamlessly to my other courses:

1. Informational questions that have nothing to do with the problem they’re working on or the material. Example: When are your office hours? When is this lab due? When is the final exam?
2. Clarifying questions that seek to make sense of the specifications of a problem. Should we use a script M-file or a function M-file here? A FOR loop or a WHILE loop? Do I have to make this plot from the command line or can I use the Plot Tools window?
3. Functional questions that are generally of the form, How do I [insert task here]?. How do I plot a function in MATLAB? How do I get the plot to be red instead of blue? How do I get this FOR loop to work?
4. Interpretive questions that seek the meaning of syntax, a command, or an error. What does MATLAB mean when it says I should ‘pre-allocate’ this variable? Why are there all these different ways to call the MAX command? Why do I have to use num2str in some situations but not in others?

I’ve tried to list these question types in increasing order of cognitive complexity, although that ordering doesn’t always hold. (Some clarifying questions can get quite complicated, for instance.) How these types of questions are ranked in this way points me in the direction of how to respond to them.

Formal informational questions are easy to answer. I always give the same, direct answer to these: It’s (on the syllabus || in the calendar || printed on your assignment). Students learn pretty quickly that this is the same answer to this kind of question all the time, so they tend to stop asking and just look it up instead, which is precisely what they should be doing.

I’m happy to give straight answers to clarifying questions, although sometimes it’s better not to. For example, if a student team is working on a program that needs a loop, and they want to know if they should use a FOR or a WHILE loop, then the best way to respond is not to tell students what to do but rather to lay out the pros and cons of each approach and let them choose.

It gets very tricky when we get to the last two types.

I let the following basic philosophy guide me: I don’t answer functional questions on labs during lab sessions or on homework while the homework is still not yet turned in. Once the lab or homework is over, then I’ll usually answer directly. But otherwise, my goal is to guide students into turning their functional question into an interpretive question. I do this through a series of Polya-like questions to the students that flows a little something like this (click to enlarge):

This is less complicated than it looks. Basically, if a student asks a functional question, I first see if the student’s done what they’re asking before. If so, they go refresh their memories. If not, they look it up in an appropriate help file until they find something that looks like what they want. Then they play with it for a minute or two to get the basic idea. Then, by that point, they either know what they’re supposed to do, or else they have a deeper, more cognitively complex question to ask, not What do I type in to do this? but Why does this work the way it does? In a freshman-level class like this one, any time I can get students to elevate themselves from functional questions to interpretive/clarifying questions, I consider it a win.

What students get out of this process is the ability to move beyond needing the professor to tell them what to do. They become self-feeders. This is important because the professor is not going to be there when they really need this stuff, two or three courses down the line or when they’re out on the job (for which they were hired because they, and nobody else around them, has these kinds of computer skills). They are getting the ability to learn on their own, which is what I consider really to be the single, primary life skill.

Unfortunately students tend to resist this process. It is not what they are used to. They are used to teachers telling them the answers to their questions, regardless of what kind of question it was, and to them a failure of a teacher to give a straight answer to their questions is tantamount to either incompetence or indifference. So this process requires a constant P.R. effort and constant clarifying about why we do things this way. And that P.R. effort doesn’t always work. I still have students who complain that I don’t answer their questions; who feel belittled when they identify that they’ve seen a command before and are asked to go back and review it; who feel questions are pointless because I’m just going to ask them more questions in return.

These are freshmen, used to a transactional model of education predominant in American high schools. The fact that this model — the teacher tells the students what to do; students follow teacher’s directions; students get good grades — is the predominant one is a serious problem in our schools, but that’s another issue. Whatever the case may be, I am getting these folks in the final four years of their formal schooling (for the most part) and if I don’t get them thinking on their own, they will crash and burn in the real world.

And I think that even if these students go on never to use MATLAB again after graduation but have a well-practiced and fluid ability to learn new and complicated things on their own, I consider that the biggest win of all. And it’s a good reason to take the MATLAB course in the first place.

Programming, lectures, and the inverted classroom

Image via Wikipedia

We started programming in the MATLAB course a couple of weeks ago. It’s been… interesting. Keep in mind that 75% of the students in the class have never written a program of any sort before; half the class rates themselves below a 6 out of 10 in “comfort level” in using computers at all. As with everything else in this course, the audience is everything.

I started this three-week unit last week with a minilecture on FOR loops. But wait, you say: I thought you were using an inverted classroom model for the MATLAB course, where students are assigned reading and viewing tasks outside of class, accompanied by homework assignments designed to help them extract the relevant information and then do simple applications of what they’ve learned. Well, yes, that’s been the plan, and the practice up until now.

But I decided to go with a minilecture/activity model for the programming unit for two reasons. One, as has been the case much of the time when putting this class together, I wasn’t finding any materials out there to give out to students on the absolute basics of MATLAB programming — by which I mean the concept of the function M-file and looping structures (we’re getting to branching structures later) — that is suitable for a total-novice audience. The Mathworks, Inc. tutorials, usually well-suited for this kind of thing, were just a little too advanced. And there just wasn’t much else out there on this subject that I’ve found that was free, online, and well-suited for this kind of thing. If you think that smells like a screencasting opportunity waiting to happen, you might be on the right track.

Secondly, the students have been struggling with this inverted classroom model even when the materials I give them are good and the subject (like curve fitting) is both familiar and pretty basic. The struggles have been mainly cultural and psychological, not intellectual. The students are plenty smart enough to pick up the basics on their own. But we’ve run into some linear combination of these issues:

• Not adopting an appropriate timetable for learning the material outside the classroom. That timetable is: get to work early on the stuff, spend small chunks of time on it, and make those chunks frequent. The ideal schedule probably comes out to: no more than 30-45 minutes at a sitting, done over the course of 5-6 days. That jives with the “2 hours outside of class for every hour inside of class” conversion factor that usually works for college. Instead, the average start time on the outside work has been less than 24 hours before the labs.
• An expectation that after watching the videos or doing the reading, we are now ready to write workable code. There has not been widespread recognition that programming, or just working with a computer system in general, is all about getting your hands dirty with stuff that is not assigned before there is a chance of doing correctly the things that are assigned. There is a certain amount of time between being exposed to information and being able to do something right with it, and that time has to be spent doing things wrong with it. The misunderstanding, common to this demographic, is that information = expertise. Get exposed to the information enough, and you’ll be good at whatever that info was about.
• A simple psychological block against the idea that basic acquisition of concepts can take place in the absence of an expert.

I asked students in a questionnaire what changes to the class would help them learn MATLAB better. Overwhelmingly (75%) the students said that a lecture before the lab activities would be helpful, even though this would mean drastically reduced time on the labs in class and therefore more time spent outside of class, which is something they (understandably) don’t want. When I asked a couple of students what they expected to get from a lecture that they can’t get through online materials, use of the class discussion board, office hours, or conversations with their lab partners, the answer was: We’d just feel better about things if you’d lecture.

So, as I said, I started the first programming class with a minilecture. I walked students through the creation of a function called sin_period:

function period = sin_period(p)
period = 2*pi/p;
x = linspace(-2*pi, 2*pi);
plot(x, sin(p*x))

So this is an unsophisticated example of how you can write a MATLAB function that does a couple of pretty different things at once. It calculates the period of where the parameter is provided by the user, and then it generates a plot of this function. Lab activity #1 given to the students: Modify this function so that the plot contains exactly two periods of 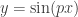and it puts a plot of 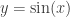on the same plot, using a dashed red line, for reference. (I really sold this to the education majors, who make up half the class, as an example of where a MATLAB function could be a useful classroom demo tool for a trigonometry or precalculus class.)

The second demo in the minilecture was using a basic FOR loop:

for i=1:10
   disp(['The square of ', num2str(i), ' is ', num2str(i^2)])
end

This was actually given out in homework during the week with the instructions to change stuff in this loop and see what happens. What is the disp command doing? What is that num2str command and why do we need it? What happens if we leave off the square brackets inside disp, and why do we get the error message we get? And above all, what does this code actually do? What would you change to get it to print out the squares of the first 20 positive integers? And so on.

I wanted this to be not so much a minilecture as a discussion among students of what they did, what they encountered, and what they learned during their code-tweaking. But it ended up being nothing but me lecturing. I’m not sure what happened. Certainly I didn’t insist on students sharing what they discovered; maybe I was getting nervous about taking up too much more lab time.

After this was over, I gave Lab activity #2: Write a function M-file called vector_diff that accepts a vector “x” as input and produces a vector “d” as output, whose entries are the differences in consecutive entries of “x”. For example, vector_diff([1 3 0 8]) should return [2 -3 8]. Of course the diff function in MATLAB already does this, and some students figured that out, but the point was to recreate that functionality from scratch to learn how a FOR loop works.

So, you ask, how did that lab turn out?

It was all over the map in terms of quality. With the sin_period activity, about half the students got it exactly right. The other half almost uniformly added in the plot of 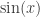with the correct color and linestyle but were unable to get the function to adjust the x-range so that two periods of show up. In other words, they were able to add in the routine stuff (just a plot command) but not able to transfer the idea of local variables within functions to use the period (which we’d already calculated) to set the x values. (All you have to do is replace x = linspace(-2*pi,2*pi) with x = linspace(-period, period).)

The FOR loop had a lot more variation. Some groups got it almost exactly right (biggest obstacle: not knowing how to add new entries to a vector). Some groups wrote code that appeared to be trying to use the right ideas, but the syntax was way off, for example using the counter variable “i” as if it were a vector (for example, using i(1):i(n) as the range on the counter). Some groups turned in nothing at all; although it turned out later that those groups had something done, but because it wasn’t exactly correct they decided to turn in nothing.

This is not a total loss, and this week (which I’ll report on later) I think we improved a lot through some more basic discussion of how to program, in general. But I take several lessons away from the results of the week 1 lab, with its much-requested lecture component:

• Lectures are only helpful to the extent that they impel students to act on what they are hearing. If you want a lecture just because you’d like an expert to assuage your misgivings about a subject — you want a lecture merely to feel better and more centered about what you’re learning — then the lecture is going to accomplish nothing other than providing a false sense of security to the students. Is this helping the student? No.
• Students who are still less than one year out of high school, where largely the opposite of what we’re doing in this class is the norm, have no idea that the first point is the case. For most students in this concrete mode of thinking, teaching = lecture = learning. This doesn’t mean they aren’t smart or capable of becoming self-supporting learners, which is sort of an overall goal of my teaching in any class. It does mean that they have to be exposed to activities that enable or require self-sufficiency, early and often. Or else they will be totally unable to function after they graduate.
• Therefore I’m more convinced than ever that the inverted classroom model for this class really is the right way to go. Give students “lectures” outside of the class time; give them time to think, questions to answer, simple tasks to perform that are based on what they read and watch. If they do it, this will generate the right questions which they can then ask (themselves, their lab partners, or me). Then they have an entire class meeting in which to do some more complicated task.
• But this only works to the extent that students adopt the short/frequent/early schedule for working on the material. If students continue to operate on the assumption that 300 minutes applied in a single 2.5-hour block late on Sunday night is the same as 300 minutes applied in five 60-minute blocks across multiple days of the week, then of course they’ll choose what appears like the lowest-footprint model and go with the single big block. But this is a flawed assumption, especially in an activity which most students self-identify as being something with which they are totally unfamiliar and largely not all that comfortable.
• This means I have to do a better job of getting students to realize this. I don’t want to start FORCING students to work this way — for example, by having teams submit journal entries or blog posts or something every couple of days. I’d rather get them to see that learning a computer tool is much more fun when you give yourself time to play, time to make and correct mistakes — time to get used to the kinds of expert behaviors that computer people employ. Incentivize rather than require.

The story continues.